Calculadora de ecuaciones cuadráticas

¿Qué son las ecuaciones cuadráticas y cómo se resuelven?

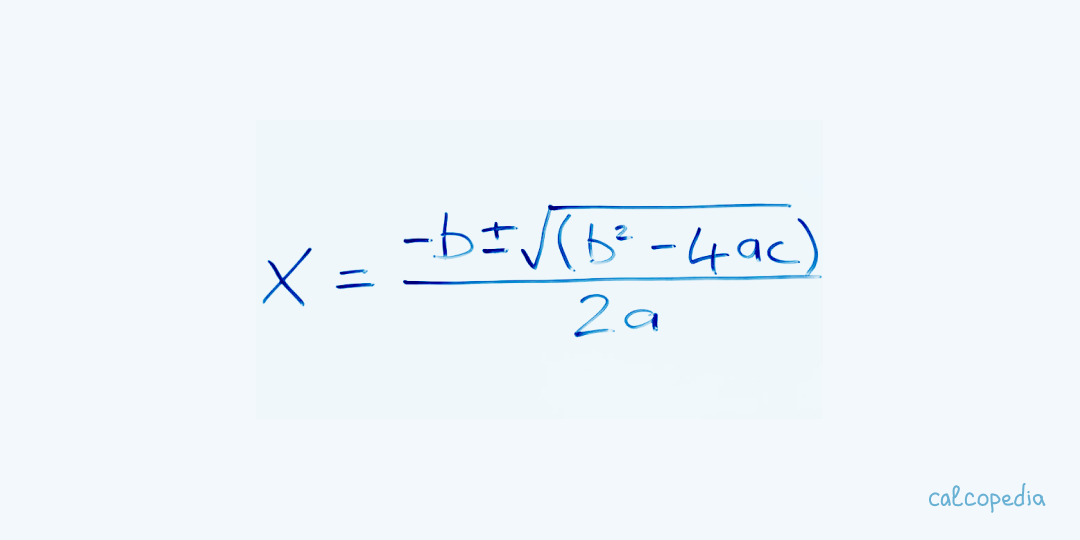
Las ecuaciones cuadráticas son ecuaciones algebraicas de la forma ax² + bx + c = 0, donde "a", "b" y "c" son coeficientes conocidos y "x" es la variable desconocida. Estas ecuaciones reciben el nombre de "cuadráticas" debido a que la variable desconocida está elevada al cuadrado.

Existen varios métodos para resolver ecuaciones cuadráticas. A continuación, explicaremos tres de los enfoques más comunes:

Fórmula general: Una forma común de resolver ecuaciones cuadráticas es utilizando la fórmula general, también conocida como fórmula cuadrática. Esta fórmula establece que las soluciones de una ecuación cuadrática pueden ser encontradas mediante la siguiente expresión:
x = (-b ± √(b² - 4ac)) / (2a)
Por ejemplo, consideremos la ecuación cuadrática 2x² - 5x + 2 = 0. Aplicando la fórmula general, obtenemos:
x = (-(-5) ± √((-5)² - 422)) / (2*2)

= (5 ± √(25 - 16)) / 4

= (5 ± √9) / 4
Por lo tanto, las soluciones son:

x1 = (5 + 3) / 4 = 2

1. = (5 - 3) / 4 = 1/2

Discriminante: Otro método común para resolver ecuaciones cuadráticas es utilizando el discriminante. El discriminante es una expresión matemática que se encuentra dentro de la fórmula cuadrática y nos proporciona información sobre las soluciones de la ecuación. Si el discriminante es positivo, la ecuación tiene dos soluciones reales distintas. Si el discriminante es cero, la ecuación tiene una única solución real. Y si el discriminante es negativo, la ecuación no tiene soluciones reales, sino soluciones complejas.
Por ejemplo, consideremos la ecuación cuadrática 3x² + 2x - 1 = 0. Calculando el discriminante, tenemos:
D = (2^2) - 43(-1)

= 4 + 12

• 16
  Como el discriminante es positivo, la ecuación tiene dos soluciones reales distintas.

Teoría de Vieta: También es posible resolver ecuaciones cuadráticas utilizando la teoría de Vieta. Esta teoría establece una relación entre los coeficientes de una ecuación cuadrática y las soluciones de la misma. De acuerdo con Vieta, la suma de las soluciones de una ecuación cuadrática es igual a -b/a, y el producto de las soluciones es igual a c/a.
Por ejemplo, consideremos la ecuación cuadrática 4x² - 7x + 3 = 0. Utilizando la teoría de Vieta, podemos obtener información sobre las soluciones:
La suma de las soluciones es x1 + x2 = -(-7)/4 = 7/4.

1. producto de las soluciones es x1 * x2 = 3/4.
   Por lo tanto, las soluciones son los valores que satisfacen estas condiciones.

Ahora que comprendemos los métodos para resolver ecuaciones cuadráticas, veamos cómo utilizar la calculadora de resolución de ecuaciones cuadráticas en línea.

¿Cómo utilizar la calculadora de resolución de ecuaciones cuadráticas?

Nuestra calculadora de resolución de ecuaciones cuadráticas es una herramienta en línea que te permite obtener las soluciones de una ecuación cuadrática de forma rápida y precisa. Sigue estos pasos para utilizarla:

1. Ingresa los coeficientes "a", "b" y "c" de la ecuación cuadrática en los campos correspondientes.
2. Selecciona el método de resolución que deseas utilizar: fórmula general, discriminante o teoría de Vieta.
3. La calculadora te mostrará las soluciones de la ecuación cuadrática.

Recuerda que debes ingresar los coeficientes correctamente y seleccionar el método de resolución adecuado para obtener resultados precisos.

Ejemplos de resolución de ecuaciones cuadráticas

Ahora, veamos algunos ejemplos prácticos de cómo resolver ecuaciones cuadráticas utilizando nuestra calculadora:

Ejemplo utilizando la fórmula general:

1. la ecuación cuadrática 2x² - 5x + 2 = 0. Aplicando la fórmula general en nuestra calculadora, obtenemos las soluciones x1 = 2 y x2 = 1/2.

Ejemplo utilizando el discriminante:

1. la ecuación cuadrática 3x² + 2x - 1 = 0. Calculando el discriminante en nuestra calculadora, encontramos que el valor es positivo. Esto significa que la ecuación tiene dos soluciones reales distintas.

Ejemplo utilizando la teoría de Vieta:

1. la ecuación cuadrática 4x² - 7x + 3 = 0. Utilizando nuestra calculadora y la teoría de Vieta, encontramos que la suma de las soluciones es 7/4 y el producto de las soluciones es 3/4.

Como puedes ver, nuestra calculadora te proporcionará las soluciones de manera rápida y precisa.

Consideraciones al resolver ecuaciones cuadráticas

Al resolver ecuaciones cuadráticas, es importante tener en cuenta ciertos aspectos para obtener resultados correctos. Aquí hay algunas consideraciones a tener en cuenta:

1. Verifica los coeficientes de la ecuación para asegurarte de que estén correctamente ingresados.
2. Determina el método de resolución adecuado según las características de la ecuación (fórmula general, discriminante o teoría de Vieta).
3. Presta atención a las operaciones algebraicas y asegúrate de realizar los cálculos correctamente.
4. Ten en cuenta el tipo de soluciones que puedes obtener: reales, complejas o nulas.
5. Si el discriminante es negativo, las soluciones serán números complejos.
6. Si obtienes una solución fraccionaria, simplifica el resultado si es necesario.
7. Verifica tus soluciones sustituyéndolas en la ecuación original para asegurarte de que sean correctas.

Calculadoras similares

Las siguientes calculadoras sobre el mismo tema podrían ser útiles para ti:

• Conversor de Sistemas Numéricos. Convierte números entre diferentes sistemas numéricos, incluyendo binario, decimal, octal y hexadecimal, de manera eficiente.
• Conversor de Hexadecimal a Decimal. Realiza conversiones de números hexadecimales a decimales de forma eficiente y precisa.
• Conversor de Hexadecimal a Binario. Convierte números hexadecimales a binarios de forma rápida y precisa.
• Conversor de Octal a Decimal. Realiza conversiones de números octales a decimales de manera eficiente y precisa.
• Conversor de Octal a Binario. Convierte números octales a binario de forma rápida y precisa, mejorando tu comprensión y análisis numéricos.
• Conversor de Decimal a Hexadecimal. Transforma números decimales en su equivalente hexadecimal, facilitando el análisis y cálculo numérico.
• Conversor de Decimal a Octal. Realiza conversiones de números decimales a octales de forma eficiente, mejorando tu comprensión numérica.
• Conversor de Decimal a Binario. Convierte números decimales a binario de forma rápida y precisa, facilitando el análisis y cálculo numérico.
• Conversor de Binario a Hexadecimal. Realiza conversiones eficientes de números binarios a su equivalente en el sistema hexadecimal.
• Conversor de Binario a Octal. Convierte números binarios a octal de forma rápida y precisa, facilitando el análisis y cálculo numérico.

Compartir en redes sociales

Si te gustó, por favor comparte la calculadora en tus plataformas de redes sociales. Es fácil para ti y beneficioso para la promoción del proyecto. ¡Gracias!