المحتوى
- 📝 ما هذا؟
- 👨🏻💻 كيف تستخدمه؟
- 📰 أمثلة
- 📑 الفروق الدقيقة
- 🤔 الأسئلة المتكررة
- 📋 المواد ذات الصلة
ما هي المعادلات التربيعية وكيفية حسابها؟
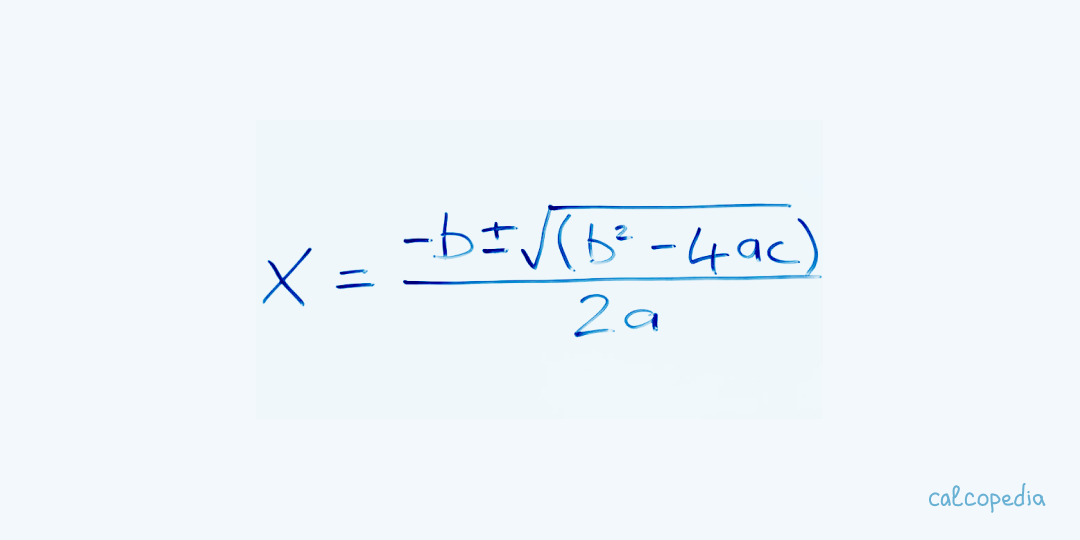
المعادلات التربيعية هي معادلات من الدرجة الثانية تأخذ الشكل العام: ax^2 + bx + c = 0 حيث a، b، وc هي أعداد حقيقية وa ≠ 0. يمكن حساب قيم x التي تحقق هذه المعادلة باستخدام مجموعة متنوعة من الأساليب. في هذه المقالة، سنتعرف على كيفية حساب المعادلات التربيعية باستخدام الصيغ الخاصة بها وعن طريق استخدام الدسكريمينانت واستنادًا إلى نظرية فييتا.
صيغة عامة للمعادلة التربيعية: ax^2 + bx + c = 0
الدسكريمينانت (D) = b^2 - 4ac
الجذور (x) = (-b ± √D) / (2a)
كيفية استخدام مُحسن الحسابات للمعادلات التربيعية؟
سيتعلم هذا القسم كيفية استخدام مُحسن الحسابات لحل المعادلات التربيعية بسهولة. يجب على المستخدمين اتباع الخطوات التالية:
- أدخل قيم a، b، وc في الحقول المعنية.
- انقر فوق زر "حساب" للحصول على النتائج.
- سيتم عرض الجذور (x) الصحيحة إذا كانت موجودة، وإلا ستظهر رسالة تفيد بعدم وجود جذور حقيقية.
أمثلة على حساب المعادلات التربيعية
فلنلقِ نظرة على ثلاثة أمثلة مختلفة لحساب المعادلات التربيعية:
المثال 1: حساب المعادلة x^2 - 4x + 4 = 0
لحساب هذه المعادلة، يمكن استخدام الدسكريمينانت للعثور على قيمة D ومن ثم استخدام الصيغة العامة لحساب الجذور. في هذه الحالة، ستكون الإجابة x = 2.
المثال 2: حساب المعادلة 3x^2 + 7x - 2 = 0
باستخدام الدسكريمينانت والصيغة العامة، يمكن حساب الجذور كالتالي: x₁ ≈ 0.29 و x₂ ≈ -2.29.
المثال 3: حساب المعادلة 2x^2 + 4x + 3 = 0
هذه المعادلة ليست لها جذور حقيقية، وستظهر رسالة بعدم وجود جذور حقيقية عند استخدام مُحسن الحسابات.
النواقص في حساب المعادلات التربيعية
عند حساب المعادلات التربيعية، يجب مراعاة بعض النقاط الهامة:
- يجب التحقق من قيمة الدسكريمينانت لمعرفة عدد الجذور ونوعها (حقيقية أو معقدة).
- إذا كان D > 0، فهناك جذران حقيقيان مختلفين.
- إذا كان D = 0، فهناك جذران متشابهان ومتساويان.
- إذا كان D < 0، فهناك جذران معقدين متشابهين.
ما هو الدسكريمينانت وكيف يؤثر على حساب المعادلات التربيعية؟
ما هو الدسكريمينانت؟
الدسكريمينانت هو معامل مهم في حساب المعادلات التربيعية، حيث يحدد عدد الجذور ونوعها. إذا كان D > 0، فهناك جذران حقيقيان مختلفين. إذا كان D = 0، فهناك جذران متشابهان ومتساويان. وإذا كان D < 0، فهناك جذران معقدين متشابهين.
كيف يمكنني حساب الدسكريمينانت؟
يمكن حساب الدسكريمينانت باستخدام الصيغة D = b^2 - 4ac حيث a، b، وc هي معاملات المعادلة التربيعية القياسية. ببساطة قم بتعويض القيم وقم بالحساب.
ماذا يعني إذا كان الدسكريمينانت سالبًا؟
إذا كان الدسكريمينانت (D) أقل من صفر، فذلك يشير إلى أن المعادلة التربيعية ليس لها جذور حقيقية. بدلاً من ذلك، ستكون الجذور معقدة ومتشابهة.
هل يمكنني استخدام مُحسن الحسابات مع قيم غير عددية؟
عذرًا، مُحسن الحسابات مصمم لحساب المعادلات التربيعية باستخدام أعداد حقيقية فقط. إذا كان لديك معادلة تحتوي على متغيرات غير عددية، فستحتاج إلى استخدام طرق أخرى لحلها.
هل هناك أي طرق أخرى لحساب المعادلات التربيعية؟
نعم، هناك طرق أخرى لحساب المعادلات التربيعية مثل الاكتمال مربعًا واستخدام جذرين مربعين. يمكنك اختيار الأسلوب الذي يناسبك بناءً على الحالة الخاصة بالمعادلة والمعرفة التي تمتلكها.
آلات حاسبة مماثلة
قد تجد الآلات الحاسبة التالية على نفس الموضوع مفيدة:
- حاسبة تحويل الملليمترات إلى بوصات. حول الملليمترات إلى بوصات بكل دقة.
- حاسبة تحويل البوصات إلى ملليمترات. حول البوصات إلى ملليمترات بكل دقة.
- حاسبة تحويل السنتيمترات إلى بوصات. حول السنتيمترات إلى بوصات بكل دقة.
- حاسبة تحويل البوصات إلى سنتيمترات. حول البوصات إلى سنتيمترات بكل دقة.
- حاسبة تحويل الأنظمة العددية. حول الأرقام بين الأنظمة العددية المختلفة بكل دقة.
- حاسبة تحويل السداسي عشر إلى العشري. حول الأرقام السداسية عشرية إلى عشرية بكل دقة.
- حاسبة تحويل السداسي عشر إلى الثنائي. حول الأرقام السداسية عشرية إلى ثنائية بكل دقة.
- حاسبة تحويل الثماني إلى العشري. حول الأرقام الثمانية إلى عشرية بكل دقة.
- حاسبة تحويل الثماني إلى الثنائي. حول الأرقام الثمانية إلى ثنائية بكل دقة.
- حاسبة تحويل العشري إلى السداسي عشر. حول الأرقام العشرية إلى سداسي عشر بكل دقة.
شارك على وسائل التواصل الاجتماعي
إذا أعجبك ذلك، يرجى مشاركة الآلة الحاسبة على منصات التواصل الاجتماعي الخاصة بك. إنه سهل بالنسبة لك ومفيد لترويج المشروع. شكراً لك!