Tool Oplossen van Kwadratische Vergelijkingen

Wat zijn kwadratische vergelijkingen en hoe bereken je ze?

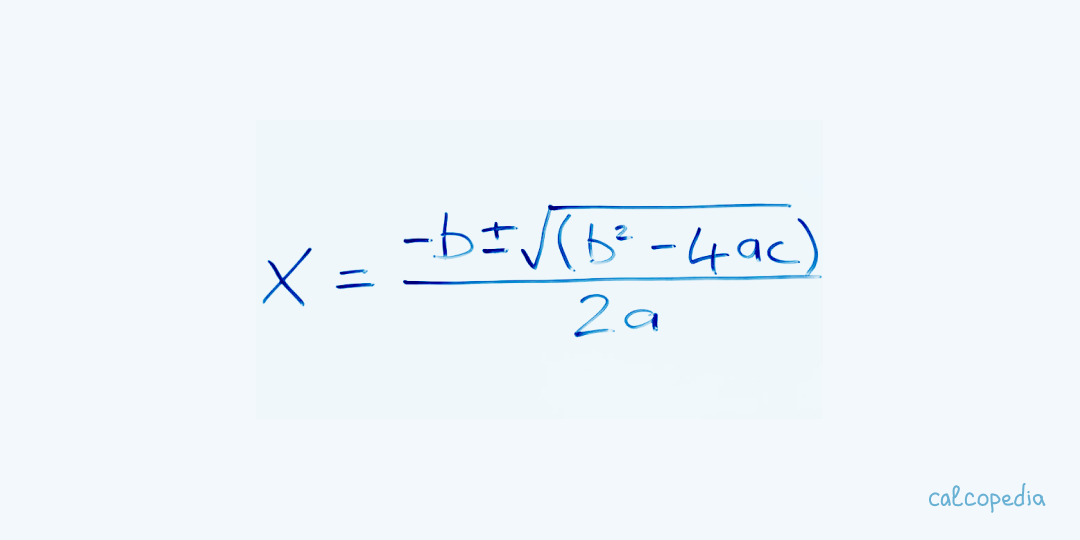
Een kwadratische vergelijking is een tweedegraads polynoomvergelijking in de vorm van ax² + bx + c = 0, waarbij 'a', 'b' en 'c' bekende waarden zijn en 'x' de onbekende variabele vertegenwoordigt. Dit type vergelijking heeft een karakteristieke 'U'-vormige grafiek, bekend als een parabool.

Om een kwadratische vergelijking op te lossen, zijn er verschillende methoden die kunnen worden toegepast, zoals factoring, het voltooien van de vierkantmethode, grafische oplossingen, en meer. Een van de meest efficiënte methoden is echter het gebruik van de kwadratische formule, ook wel bekend als de ABC-formule.

De kwadratische formule is als volgt: x = (-b ± √(b²-4ac)) / (2a). Deze formule geeft de oplossingen van een kwadratische vergelijking door direct de waarden van 'x' te berekenen, ook bekend als de wortels van de vergelijking. Deze wortels kunnen reëel of complex zijn, afhankelijk van de discriminant (b²-4ac).

Hoe gebruik je de rekenmachine voor kwadratische vergelijkingen?

De online rekenmachine voor kwadratische vergelijkingen is een handig hulpmiddel dat het oplossen van deze vergelijkingen versnelt en vereenvoudigt. Hier volgt een stapsgewijze handleiding voor het gebruik ervan:

1. Open de rekenmachine: Ga naar de website waar de rekenmachine voor kwadratische vergelijkingen zich bevindt. Je ziet direct invoervelden voor je vergelijking.

2. Voer de waarden in: In de daarvoor bestemde velden voer je de coëfficiënten 'a', 'b', en 'c' van je kwadratische vergelijking in.

3. Bereken: Nadat je de waarden hebt ingevoerd, klik je op de knop 'Berekenen' of een vergelijkbare knop om het proces te starten.

4. Bekijk de resultaten: De rekenmachine toont je de wortels van de vergelijking, ofwel de waarden van 'x'. Afhankelijk van de discriminant kunnen dit twee verschillende wortels zijn, één enkele wortel, of geen reële wortels.

5. Extra informatie: In sommige gevallen biedt de rekenmachine extra informatie, zoals de discriminant, de vertex van de parabool, en zelfs de grafiek van de vergelijking.

6. Nieuwe vergelijkingen: Voor een nieuwe berekening, klik op de knop 'Reset' of voer nieuwe waarden in voor een andere vergelijking.

Voorbeelden van het berekenen van kwadratische vergelijkingen

Het oplossen van kwadratische vergelijkingen kan behoorlijk abstract lijken, dus laten we enkele praktische voorbeelden bekijken om te zien hoe dit in het echte leven kan worden toegepast.

Voorbeeld 1: De stuiterende bal - Stel je een bal voor die van een bepaalde hoogte wordt gedropt en elke keer een hoogte bereikt die 50% is van de vorige hoogte. Als de bal van 10 meter hoog wordt gedropt, hoe vaak zal de bal dan stuiteren voordat het minder dan 1 meter hoog springt? Hier kunnen we een kwadratische vergelijking gebruiken om het aantal stuiteren te bepalen.

Voorbeeld 2: De winstgevende verkoop - Stel je een bedrijf voor dat producten verkoopt met een variabele prijs. De vraag naar het product is afhankelijk van de prijs volgens een kwadratische vergelijking. Het bedrijf wil de prijs bepalen die de maximale winst zal opleveren. Door de kwadratische vergelijking op te lossen, kunnen we de optimale prijs voor het product bepalen.

Voorbeeld 3: De raketlancering - Een raket wordt gelanceerd en de hoogte van de raket kan worden gemodelleerd door een kwadratische vergelijking. Het ruimteagentschap wil weten wanneer de raket een hoogte van 100 km bereikt, de zogenaamde Karmanlijn, waar de ruimte officieel begint. Door de kwadratische vergelijking op te lossen, vinden we het tijdstip waarop de raket deze hoogte bereikt.

Nuances bij het berekenen van kwadratische vergelijkingen

Bij het oplossen van kwadratische vergelijkingen zijn er verschillende nuances en overwegingen om in gedachten te houden. Hier zijn enkele belangrijke punten:

1. Discriminant: De waarde van de discriminant (b²-4ac) bepaalt het aantal en het type oplossingen (reëel of complex).
2. Volledige vierkanten: Soms is het voltooien van de vierkantmethode een meer geschikte strategie, vooral als de vergelijking niet gemakkelijk te factoriseren is.
3. Grafische interpretatie: Begrijpen hoe de vergelijking zich vertaalt naar een parabool op een grafiek kan helpen bij het visualiseren van de oplossingen.
4. Nul coëfficiënt: Als de 'a'-coëfficiënt nul is, degradeert de vergelijking tot een lineaire vergelijking, omdat er geen kwadratische term is.
5. Factoring: Voor vergelijkingen die gemakkelijk te factoriseren zijn, kan factoring een snelle oplossingsmethode zijn.
6. Nauwkeurigheid: Bij het gebruik van een rekenmachine, zorg ervoor dat je de coëfficiënten correct invoert om nauwkeurige resultaten te garanderen.
7. Praktische toepassingen: Overweeg de context van de vergelijking, aangezien sommige oplossingen mogelijk geen praktische betekenis hebben in de echte wereld.
8. Complexiteit: Voor complexere vergelijkingen kunnen aanvullende of meer geavanceerde methoden nodig zijn.

Vergelijkbare rekenmachines

De volgende rekenmachines over hetzelfde onderwerp kunnen nuttig zijn:

• Millimeters naar Inches. Zet lengte om van millimeters naar inches.
• Inches naar Millimeters. Zet lengte om van inches naar millimeters.
• Centimeters naar Inches. Zet lengte om van centimeters naar inches.
• Inches naar Centimeters. Zet lengte om van inches naar centimeters.
• Nummersysteem Conversie. Zet getallen om tussen verschillende nummersystemen.
• Hexadecimaal naar Decimaal. Zet hexadecimale getallen om naar decimale getallen.
• Hexadecimaal naar Binair. Zet hexadecimale getallen om naar binaire getallen.
• Octaal naar Decimaal. Zet octale getallen om naar decimale getallen.
• Octaal naar Binair. Zet octale getallen om naar binaire getallen.
• Decimaal naar Hexadecimaal. Zet decimale getallen om naar hexadecimale getallen.

Delen op sociale media

Als je het leuk vindt, deel dan de rekenmachine op je sociale mediaplatforms. Het is eenvoudig voor jou en voordelig voor de promotie van het project. Bedankt!