Quadratische Gleichungsrechner

Inhalt

📝 Was ist das?
👨🏻‍💻 Wie benutzt man das?
📰 Beispiele
📑 Nuancen
🤔 Häufig gestellte Fragen
📋 Verwandte Materialien

Was sind quadratische Gleichungen und wie werden sie gelöst?

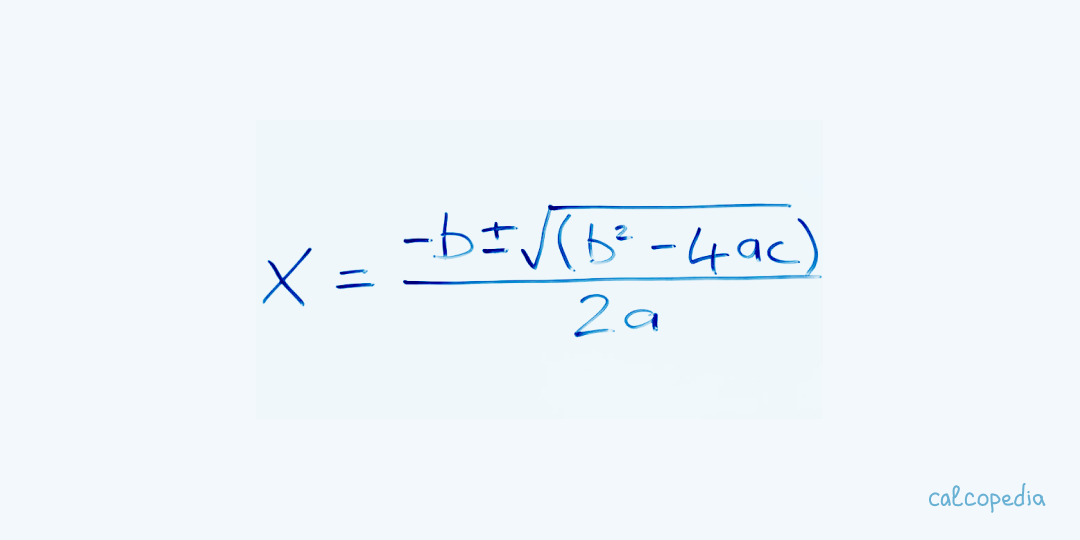
Quadratische Gleichungen Rechner

Quadratische Gleichungen gehören zu den grundlegendsten und am häufigsten auftretenden mathematischen Problemen. Eine quadratische Gleichung ist eine Gleichung zweiten Grades, die die Form ax² + bx + c = 0 hat, wobei a, b und c Konstanten sind und a ≠ 0.

Es gibt verschiedene Methoden, um quadratische Gleichungen zu lösen. Die häufigsten sind die Lösung mittels Quadratwurzel, die Faktorisierung, das Komplettieren der Quadrat, die Verwendung der Quadratischen Formel und die Anwendung der Vietas Theoreme.

Der Quadratische Formel basiert auf der Diskriminante (D = b² - 4ac). Wenn D größer als Null ist, hat die Gleichung zwei unterschiedliche Lösungen. Wenn D gleich Null ist, hat die Gleichung eine doppelte Lösung. Wenn D kleiner als Null ist, hat die Gleichung keine Lösungen in den reellen Zahlen.

Die Vietas Theoreme bieten eine andere Möglichkeit, quadratische Gleichungen zu lösen. Sie beziehen sich auf die Beziehung zwischen den Koeffizienten der Gleichung und ihren Lösungen.

Wie benutzt man den Rechner zur Lösung quadratischer Gleichungen?

Unser Online-Rechner zur Lösung quadratischer Gleichungen ist einfach zu bedienen und liefert schnelle, genaue Ergebnisse. Hier ist eine Schritt-für-Schritt-Anleitung.

Geben Sie die Koeffizienten a, b und c der quadratischen Gleichung in die entsprechenden Felder ein.
Der Rechner bestimmt die Diskriminante und gibt die Art der Lösungen an.
Je nach Wert der Diskriminante zeigt der Rechner eine, zwei oder keine Lösungen an.
Die Lösungen werden sowohl mit der Quadratischen Formel als auch mit den Vietas Theoremen angezeigt.
Der Rechner bietet auch eine detaillierte Erklärung für jeden Schritt im Lösungsprozess.

Beispielhafte Lösungen quadratischer Gleichungen

Hier sind drei praktische Beispiele für die Lösung quadratischer Gleichungen:

Beispiel: Ein Ball wird senkrecht nach oben geworfen. Die Höhe des Balls zu einem bestimmten Zeitpunkt t wird durch die quadratische Gleichung h(t) = -16t² + 40t + 6 beschrieben. Um die maximale Höhe des Balls zu berechnen, können Sie den Koeffizienten a, b und c in den Kalkulator eingeben und die Methode der quadratischen Lösungsformeln verwenden.
Beispiel: Ein Quadrat hat einen Flächeninhalt von 25 Quadratmetern. Um die Länge der Seiten des Quadrats zu berechnen, können Sie die Gleichung A = x² verwenden, wobei A der Flächeninhalt ist. Geben Sie den Koeffizienten a, b und c in den Kalkulator ein und verwenden Sie die Diskriminante, um die Lösungen zu erhalten.
Beispiel: Ein Auto fährt mit einer Geschwindigkeit von v km/h. Die Bremswege Distanz des Autos wird durch die Gleichung d(v) = 0,05V² + 0,2v beschrieben. Um die Geschwindigkeit zu berechnen, bei der der Bremsweg Distanz 50 Meter beträgt, geben Sie die Koeffizienten in den Kalkulator ein und verwenden Sie die Vietaschen Formel, um die Lösungen zu finden.

Berechnung Nuancen quadratischer Gleichungen

Bei der Lösung quadratischer Gleichungen sollten Sie folgende Punkte beachten:

Stellen Sie sicher, dass Ihre Gleichung in der Standardform ax² + bx + c = 0 ist.
Überprüfen Sie, ob a ≠ 0 ist, da es sonst keine quadratische Gleichung ist.
Beachten Sie, dass eine Diskriminante, die kleiner als Null ist, darauf hinweist, dass die Gleichung keine reellen Lösungen hat.
Seien Sie vorsichtig bei der Wurzelberechnung in der Quadratischen Formel.
Berücksichtigen Sie, dass die Vietas Theoreme nur für Gleichungen gelten, die in der Form x² - (Summe der Wurzeln)x + Produkt der Wurzeln = 0 vorliegen.
Beachten Sie, dass das Vorzeichen vor den Wurzeln in der Vietas Formeln umgekehrt ist.
Beachten Sie, dass der Rechner auch komplexe Lösungen für Gleichungen mit einer negativen Diskriminante berechnen kann.

❓ Häufig gestellte Fragen zur Lösung quadratischer Gleichungen

Hier sind einige häufig gestellte Fragen und ihre Antworten zur Lösung quadratischer Gleichungen:

Gibt es eine Möglichkeit, quadratische Gleichungen ohne den Einsatz von Formeln oder Kalkulatoren zu lösen?

Ja, es gibt verschiedene geometrische Methoden, um quadratische Gleichungen grafisch oder durch Faktorisierung zu lösen. Jedoch bieten Formeln und Kalkulatoren eine schnellere und genauere Lösung.

Wie erkenne ich, ob eine quadratische Gleichung zwei reale Lösungen oder komplexe Lösungen hat?

Überprüfen Sie das Vorzeichen der Diskriminante. Wenn die Diskriminante positiv ist, hat die Gleichung zwei reale Lösungen. Wenn sie negativ ist, hat die Gleichung zwei komplexe Lösungen. Wenn die Diskriminante null ist, hat die Gleichung eine doppelte reale Lösung.

Können quadratische Gleichungen mehr als zwei Lösungen haben?

Nein, quadratische Gleichungen haben immer entweder zwei reale Lösungen, eine doppelte reale Lösung oder zwei komplexe Lösungen.

Wofür werden quadratische Gleichungen in der realen Welt verwendet?

Quadratische Gleichungen haben vielfältige Anwendungen, wie zum Beispiel bei der Berechnung von Bewegungsdetails von Objekten, Flächenberechnungen, Finanzanalysen und vielem mehr.

Kann der Kalkulator auch quadratische Gleichungen mit rationalen Koeffizienten lösen?

Ja, der Kalkulator kann quadratische Gleichungen mit beliebigen rationalen Koeffizienten lösen, solange die Eingaben korrekt sind und die Gleichungen lösbar sind.

In sozialen Medien teilen

Wenn es Ihnen gefallen hat, teilen Sie bitte den Rechner auf Ihren sozialen Medien. Es ist einfach für Sie und nützlich für die Promotion des Projekts. Danke!

Calcopedia (de) → Quadratische Gleichungen