Calcolatore Equazioni Quadratiche

Cosa sono le equazioni quadratiche e come si calcolano?

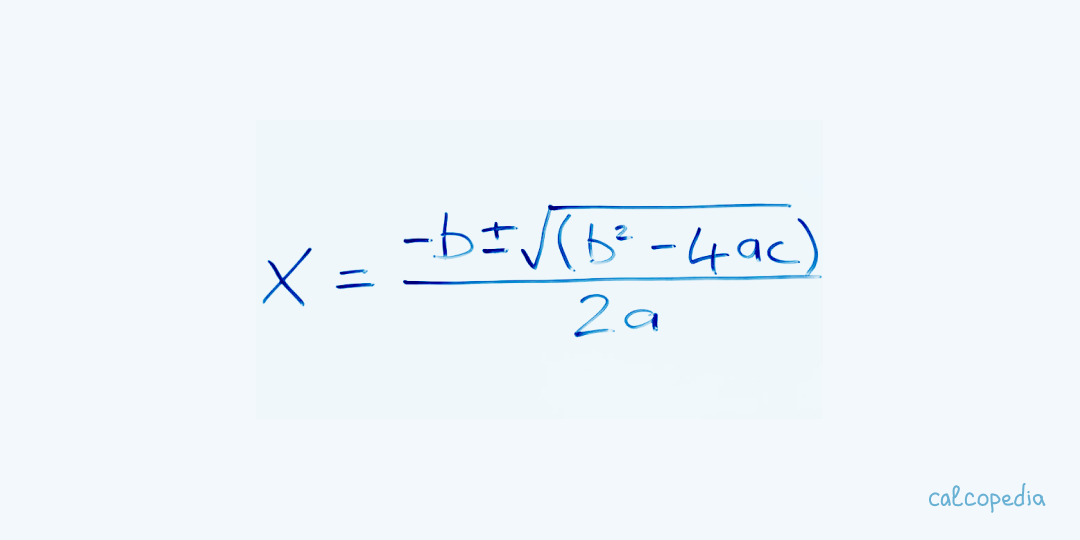
Un'equazione quadratica è un'equazione del secondo grado che ha la forma generale ax² + bx + c = 0, dove a, b e c sono coefficienti e "a" non può essere uguale a zero, perché altrimenti l’equazione sarebbe di primo grado. Queste equazioni sono fondamentali in molti ambiti scientifici e ingegneristici.

Calcolare le soluzioni di un'equazione quadratica, conosciute anche come radici, significa trovare i valori di x che soddisfano l’equazione. Questo è fondamentale in molte discipline, dalla fisica all’ingegneria, e anche nella vita quotidiana.

La soluzione di un'equazione quadratica può essere trovata usando la formula quadratica x = (-b ± √(b² - 4ac)) / (2a), conosciuta anche come formula risolutiva generale. Il termine sotto la radice, b² - 4ac, è noto come discriminante e determina la natura delle radici dell’equazione.

Un'altra metodologia per risolvere queste equazioni è attraverso l’applicazione del teorema di Viete, che permette di trovare le radici sfruttando le relazioni tra i coefficienti dell’equazione e le sue radici.

Come utilizzare il calcolatore di equazioni quadratiche?

Il calcolatore di equazioni quadratiche è uno strumento online intuitivo e facile da usare che fornisce le soluzioni delle equazioni quadratiche in modo rapido e accurato. Ecco una guida passo-passo su come usarlo:

1. Inserisci i coefficienti a, b e c dell’equazione quadratica nella forma ax² + bx + c nei campi corrispondenti del calcolatore.
2. Assicurati che i valori inseriti siano corretti. Ricorda che il coefficiente "a" non può essere zero.
3. Premi il pulsante "Calcola" o una funzione simile per avviare il processo di calcolo.
4. Il calcolatore mostrerà le radici dell’equazione, se esistenti, utilizzando la formula quadratica. In caso di radici complesse, verranno presentate nella forma appropriata.
5. Inoltre, il calcolatore può fornire informazioni sul discriminante, indicando se le radici sono reali, uguali o complesse.
6. Se disponibile, potresti anche ricevere una rappresentazione grafica dell’equazione, mostrando dove l’equazione interseca l’asse x, cioè le radici.
7. Per equazioni successive, ripeti il processo da capo. Alcuni calcolatori offrono anche la possibilità di risolvere sistemi di equazioni quadratiche.

Esempi di risoluzione di equazioni quadratiche

Le equazioni quadratiche compaiono in svariati contesti della vita reale, dai calcoli finanziari alla fisica applicata. Vediamo alcuni esempi pratici e divertenti:

1. Il salto del paracadutista: Supponiamo che un paracadutista salti da un'altura e la sua altezza in relazione al tempo sia rappresentata da h(t) = -5t² + 50t + 100, dove h è l’altezza (in metri) e t il tempo (in secondi). Per scoprire dopo quanto tempo il paracadutista raggiungerà il suolo, dobbiamo risolvere l’equazione ponendo h(t) uguale a zero e risolvendola per t. Con un pizzico di adrenalina in più, scopriamo che il tempo per il "faccia a terra" è... (usa il calcolatore per scoprirlo!)
2. La fabbrica di gelati: Una fabbrica produce coni gelato con un volume che può essere calcolato come V(r) = (1/3)πr²h, dove r è il raggio della base e h l’altezza. Volendo massimizzare il gelato nel cono senza aumentare il materiale usato per il cono stesso, potremmo usare le equazioni quadratiche per trovare il raggio ottimale. È un dilemma deliziosamente difficile!
3. l’investimento azionario: Supponendo che il profitto di un investimento azionario possa essere rappresentato da P(x) = -7x² + 100x - 200, dove x sono i mesi, potremmo voler scoprire dopo quanti mesi otterremo il massimo profitto o se dovremmo ritirarci prima di finire in perdita. Un caso classico di "montagne russe finanziarie"!

Sfumature nel calcolo delle equazioni quadratiche

Nel calcolare le equazioni quadratiche, è importante considerare vari fattori che possono influenzare il risultato. Ecco alcuni punti da tenere a mente:

• Il discriminante determina la natura delle radici. Se è positivo, ci sono due radici reali e distinte; se è zero, ci sono due radici reali e uguali; se è negativo, le radici sono complesse.
• Se il coefficiente a è zero, l’equazione non è più quadratica ma lineare.
• Nelle applicazioni reali, i coefficienti a, b e c devono essere interpretati nel contesto del problema specifico.
• Le unità di misura (se presenti) devono essere coerenti in tutta l’equazione e nei calcoli successivi.
• Nel caso di radici complesse, è importante comprendere il concetto di numeri complessi e come vengono rappresentati.
• La rappresentazione grafica di un'equazione quadratica è una parabola; conoscere la direzione e la forma della parabola può aiutare nella comprensione del problema.
• Utilizzando metodi numerici per approssimare le radici, come il metodo di Newton o il metodo di bisezione, si deve essere consapevoli dell’errore di approssimazione.
• Quando si usano calcolatori o software per risolvere equazioni quadratiche, è essenziale comprendere i limiti e le potenzialità dello strumento utilizzato.
• È importante verificare le soluzioni ottenute, inserendole nell’equazione originale per assicurarsi che la rendano un'identità.

Calcolatrici simili

Potresti trovare utili le seguenti calcolatrici sullo stesso argomento:

• Convertitore da Millimetri a Pollici Online. Converti misure da millimetri a pollici in modo rapido e accurato con il nostro calcolatore online.
• Convertitore da Pollici a Millimetri Online. Converti misure da pollici a millimetri in modo rapido e accurato con il nostro calcolatore online.
• Convertitore da Centimetri a Pollici Online. Converte misure da centimetri a pollici con facilità e precisione usando il nostro calcolatore online.
• Convertitore da Pollici a Centimetri Online. Converti misure da pollici a centimetri rapidamente e con precisione con il nostro calcolatore online.
• Convertitore di Sistemi Numerici Online. Utilizza il nostro calcolatore online per convertire numeri tra diversi sistemi numerici in modo efficiente e accurato.
• Convertitore da Esadecimale a Decimale Online. Converti numeri esadecimali in decimali facilmente e con precisione usando il nostro calcolatore online.
• Convertitore da Esadecimale a Binario Online. Converti numeri esadecimali in binari rapidamente e con precisione con il nostro calcolatore online.
• Convertitore da Ottale a Decimale Online. Converti numeri ottali in decimali con facilità e precisione usando il nostro calcolatore online.
• Convertitore da Ottale a Binario Online. Converti numeri ottali in binari in modo efficiente con il nostro calcolatore online.
• Convertitore da Decimale a Esadecimale Online. Converti numeri decimali in esadecimali con precisione e facilità usando il nostro calcolatore online.

Condividi sui social media

Se ti è piaciuto, condividi la calcolatrice sui tuoi social media. È facile per te e utile per la promozione del progetto. Grazie!