Conteúdo
- 📝 O que é isso?
- 👨🏻💻 Como usar?
- 📰 Exemplos
- 📑 Nuanças
- 🤔 Perguntas frequentes
- 📋 Materiais relacionados
O que são equações quadráticas e como elas são resolvidas?
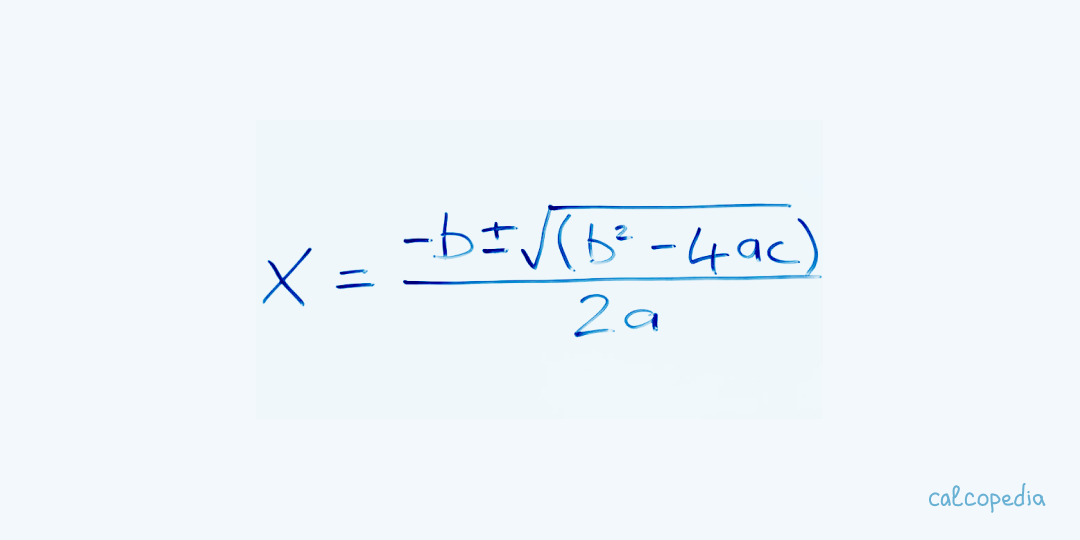
As equações quadráticas são equações polinomiais de segundo grau, geralmente escritas na forma ax² + bx + c = 0, onde "a", "b" e "c" são coeficientes conhecidos, e "x" é a variável desconhecida que queremos encontrar. Essas equações podem ter zero, uma ou duas soluções reais, dependendo do valor do discriminante.
Existem três principais maneiras de resolver equações quadráticas:
- Fórmula Quadrática: Usando a fórmula geral x = (-b ± √(b² - 4ac)) / 2a, onde √ representa a raiz quadrada.
- Método do Discriminante: Calculando o discriminante Δ = b² - 4ac e usando suas propriedades para determinar a natureza das soluções.
- Teorema de Viète: Somando e multiplicando as raízes para encontrar as somas e produtos das soluções.
Como usar o Calculadora de Equações Quadráticas?
O "Calculadora de Equações Quadráticas" é uma ferramenta online concebida para facilitar o processo de resolução de equações quadráticas. Para utilizá-lo, basta acessar o site da calculadora em seu navegador.
Na interface da calculadora, você encontrará três campos onde deve inserir os coeficientes da equação quadrática ax² + bx + c = 0. Digite os valores de "a", "b" e "c" nas respectivas caixas. É importante verificar se os coeficientes estão corretos antes de prosseguir.
A calculadora irá processar os coeficientes fornecidos e aplicar o método adequado para resolver a equação quadrática.
O resultado será exibido na tela, mostrando as soluções da equação, o valor do discriminante (se aplicável) e, se for o caso, as somas e produtos das raízes. Se a equação tiver soluções reais, elas serão exibidas na forma x₁ e x₂.
Lembre-se de verificar suas respostas, substituindo as raízes encontradas na equação original para garantir que estejam corretas. Caso necessário, você pode limpar os campos e repetir o processo para resolver outras equações quadráticas.
Exemplos de resolução de equações quadráticas
Portanto, vamos seguir para nossos exemplos e ver como essa poderosa ferramenta pode ajudá-lo a resolver facilmente equações quadráticas encontradas em vários problemas matemáticos e situações da vida real.
- Resolvendo a equação quadrática 2x² - 5x + 2 = 0 usando a fórmula quadrática:
a = 2, b = -5, c = 2
Aplicando a fórmula: x = (-(-5) ± √((-5)² - 422)) / 2*2
x = (5 ± √(25 - 16)) / 4
x = (5 ± √9) / 4
x = (5 ± 3) / 4
Portanto, as soluções são: x₁ = (5 + 3) / 4 = 2 e x₂ = (5 - 3) / 4 = 1/2
- Encontrando as soluções da equação quadrática x² + 6x + 9 = 0 usando o método do discriminante:
a = 1, b = 6, c = 9
Calculando o discriminante: Δ = 6² - 419 = 36 - 36 = 0
O discriminante é igual a zero, o que significa que a equação tem uma solução real dupla.
Usando a fórmula x = -b / 2a: x = -6 / 2*1 = -3
Portanto, a única solução é x = -3.
- Utilizando o teorema de Viète para resolver a equação quadrática 3x² - 8x + 4 = 0:
a = 3, b = -8, c = 4
As somas das raízes são dadas por: S = -b / a = -(-8) / 3 = 8/3
Os produtos das raízes são dados por: P = c / a = 4 / 3
Portanto, as raízes são tais que sua soma é 8/3 e seu produto é 4/3.
Nuanças no cálculo de equações quadráticas
Ao resolver equações quadráticas, é importante estar ciente de algumas nuanças que podem surgir durante o processo de cálculo:
- O discriminante Δ determina a natureza das raízes. Δ > 0 indica duas raízes reais e distintas, Δ = 0 indica duas raízes reais e iguais, e Δ < 0 indica duas raízes complexas conjugadas.
- Se "a" for igual a zero, a equação não será mais quadrática.
- Quando as raízes são números irracionais, as soluções devem ser arredondadas para um número adequado de casas decimais.
- Se o discriminante for um quadrado perfeito, as raízes serão números inteiros.
- Verifique sempre as respostas substituindo as raízes encontradas na equação original para garantir que elas estejam corretas.
❓ Perguntas frequentes sobre a resolução de equações quadráticas
Aqui estão as respostas para algumas das perguntas mais frequentes sobre a resolução de equações quadráticas. Essas perguntas e respostas irão ajudá-lo a compreender melhor o processo de resolver equações quadráticas e esclarecer quaisquer dúvidas que possam surgir.
Como posso saber quantas raízes uma equação quadrática tem?
O número de raízes reais de uma equação quadrática é determinado pelo valor do discriminante (Δ). Δ > 0 indica duas raízes reais e distintas, Δ = 0 indica duas raízes reais e iguais, e Δ < 0 indica duas raízes complexas conjugadas.
Posso resolver uma equação quadrática sem usar a fórmula quadrática?
Sim, além da fórmula quadrática, você pode usar o método do discriminante e o teorema de Viète para resolver equações quadráticas.
As equações quadráticas sempre têm soluções reais?
Nem sempre. Se o discriminante (Δ) for negativo, a equação não terá soluções reais, mas sim soluções complexas conjugadas.
Há alguma dica para fatorar equações quadráticas facilmente?
Nem todas as equações quadráticas podem ser fatoradas facilmente. A fórmula quadrática ou o método do discriminante são frequentemente usados para encontrar soluções em tais casos.
O que fazer se a equação tiver coeficientes fracionários?
Se a equação tiver coeficientes fracionários, é recomendável eliminar as frações multiplicando toda a equação por um fator adequado que a torne uma equação de coeficientes inteiros antes de aplicar qualquer método de resolução.
Calculadoras similares
Você pode achar as seguintes calculadoras sobre o mesmo tema úteis:
- Calculador de Conversão entre Sistemas Numéricos. Converta números entre sistemas binário, decimal, octal e hexadecimal de forma rápida e fácil com nosso calculador online.
- Calculador de Conversão de Hexadecimal para Decimal. Converta números hexadecimais em decimais de maneira rápida e precisa com nosso calculador online.
- Calculador de Conversão de Hexadecimal para Binário. Transforme números hexadecimais em binários facilmente com nosso calculador online.
- Calculador de Conversão de Octal para Decimal. Mude números octais para decimais rapidamente com nosso calculador de conversão.
- Calculador de Conversão de Octal para Binário. Converta números octais em binários de maneira rápida e precisa com nosso calculador online.
- Calculador de Conversão de Decimal para Hexadecimal. Transforme números decimais em hexadecimais facilmente com nosso calculador online.
- Calculador de Conversão de Decimal para Octal. Converta números decimais em octais de maneira rápida e precisa com nosso calculador online.
- Calculador de Conversão de Decimal para Binário. Transforme números decimais em binários facilmente com nosso calculador online.
- Calculador de Conversão de Binário para Hexadecimal. Mude números binários para hexadecimais rapidamente com nosso calculador de conversão.
- Calculador de Conversão de Binário para Octal. Converta facilmente números binários em octais com nosso calculador online.
Compartilhe nas redes sociais
Se você gostou, por favor, compartilhe a calculadora em suas plataformas de mídia social. É fácil para você e benéfico para a promoção do projeto. Obrigado!