Содержание
Что такое квадратные уравнения и как это вычислить?
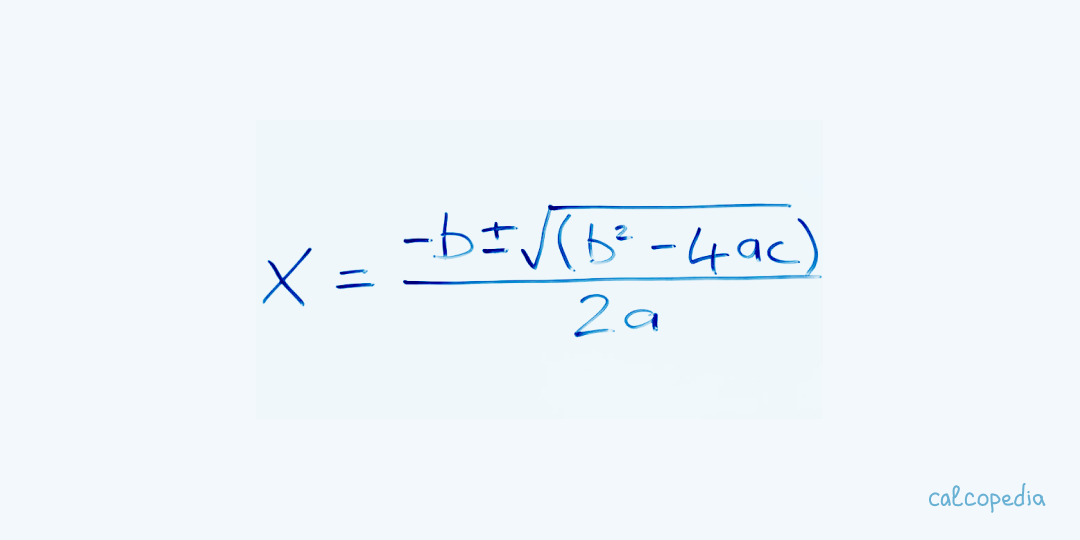
Квадратное уравнение – это уравнение второй степени, имеющее вид ax² + bx + c = 0, где a, b и c — известные коэффициенты, а x — неизвестное. Коэффициент a не равен нулю, иначе уравнение перестаёт быть квадратным.
x₁,₂ = (-b ± √D) / 2a
Здесь D - это дискриминант, который рассчитывается по формуле: D = b² - 4ac. Зависимо от значения дискриминанта, квадратное уравнение может иметь два, один или ни одного действительных корня.
Решение квадратных уравнений – классическая задача, которую учат в школе, и понимание её помогает в решении многих практических проблем.
Как использовать калькулятор квадратных уравнений?
Наш онлайн-калькулятор создан для упрощения процесса решения квадратных уравнений. Следуйте этому пошаговому руководству, и вы быстро найдёте корни вашего уравнения!
1. Откройте калькулятор и введите коэффициенты a, b и c в соответствующие поля.
2. Нажмите кнопку «Решить».
3. После короткой обработки на экране отобразятся корни вашего уравнения (или сообщение о том, что действительных корней нет).
4. Если вы хотите узнать дискриминант, воспользуйтесь соответствующей функцией калькулятора.
5. Для решения другого уравнения просто введите новые коэффициенты и повторите процесс.
6. Калькулятор также предоставляет опцию для решения уравнения по теореме Виета. Для этого выберите соответствующий режим.
7. Пользуйтесь и наслаждайтесь математикой!
Примеры расчета квадратных уравнений
Ниже приведены живые примеры решения квадратных уравнений. Будет весело, обещаю!
Пример 1: Решим уравнение x² - 5x + 6 = 0. Дискриминант D = 25 - 24 = 1. Корни уравнения: x₁ = 3, x₂ = 2. Вот и всё! Кто сказал, что математика сложная?
Пример 2: Попробуем уравнение x² + x - 6 = 0. Здесь D = 1 + 24 = 25. У нас два корня: x₁ = 2 и x₂ = -3. Математика – это как велосипед: падать можно, но главное – продолжать ехать!
Пример 3: Возьмём уравнение x² + 4x + 5 = 0. Дискриминант D = 16 - 20 = -4. Увы, действительных корней нет. Но не расстраивайтесь, ведь в математике есть и комплексные числа!
Нюансы расчета квадратных уравнений
Как и в любой науке, в математике есть свои нюансы. Давайте рассмотрим некоторые из них:
1. Если дискриминант отрицательный, у уравнения нет действительных корней.
2. Если дискриминант равен нулю, у уравнения один корень.
3. Коэффициент a не может быть равен нулю. В противном случае это не квадратное уравнение.
4. Уравнение вида x² = 0 имеет единственный корень x = 0.
5. Используя теорему Виета, можно быстро найти корни уравнения без вычисления дискриминанта.
6. Не забывайте про комплексные корни, если дискриминант отрицательный!
7. При решении уравнений по теореме Виета помните о правильном знаке перед корнями.
8. Не все квадратные уравнения имеют действительные корни.
9. Для того чтобы уравнение было квадратным, хотя бы один коэффициент должен быть отличным от нуля.
10. Всегда проверяйте полученные корни, подставив их в исходное уравнение.
Часто задаваемые вопросы о расчете квадратных уравнений
Зачем мне решать квадратные уравнения?
Квадратные уравнения часто возникают в реальной жизни, например, при проектировании мостов, расчетах финансов и даже в астрономии!
Что делать, если дискриминант отрицательный?
Это означает, что у уравнения нет действительных корней. Однако у него есть комплексные корни, которые можно найти, используя мнимую единицу.
Можно ли решить квадратное уравнение без калькулятора?
Да, можно! Используйте классическую формулу квадратного уравнения или теорему Виета.
Почему коэффициент 'a' не может быть равен нулю?
Если 'a' равно нулю, уравнение становится линейным, а не квадратным.
Может ли квадратное уравнение иметь больше двух корней?
Нет, квадратное уравнение может иметь максимум два корня. Если дискриминант равен нулю, то у уравнения один корень.
Похожие калькуляторы
Вам могут пригодиться следующие калькуляторы на эту же тему:
- Калькулятор перевода скорости из м/с в км/ч. Введите скорость в метрах в секунду для перевода в километры в час.
- Калькулятор перевода скорости из км/ч в м/с. Введите скорость в километрах в час для перевода в метры в секунду.
- Калькулятор перевода систем счисления. Введите число и выберите системы счисления для его перевода.
- Калькулятор перевода из шестнадцатеричной в десятичную. Введите шестнадцатеричное число для его перевода в десятичное.
- Калькулятор перевода из шестнадцатеричной в двоичную. Введите шестнадцатеричное число для его перевода в двоичное.
- Калькулятор перевода из восьмеричной в десятичную. Введите восьмеричное число для его перевода в десятичное.
- Калькулятор перевода из восьмеричной в двоичную. Введите восьмеричное число для его перевода в двоичное.
- Калькулятор перевода из десятичной в шестнадцатеричную. Введите десятичное число для его перевода в шестнадцатеричное.
- Калькулятор перевода из десятичной в восьмеричную. Введите десятичное число для его перевода в восьмеричное.
- Калькулятор перевода из десятичной в двоичную. Введите десятичное число для его перевода в двоичное.
Поделиться в социальных сетях
Если вам понравилось, пожалуйста, поделитесь этим калькулятором в социальных сетях. Это просто для вас и полезно для продвижения проекта. Спасибо!