Калькулятор квадратних рівнянь

Що таке квадратні рівняння та як їх обчислити?

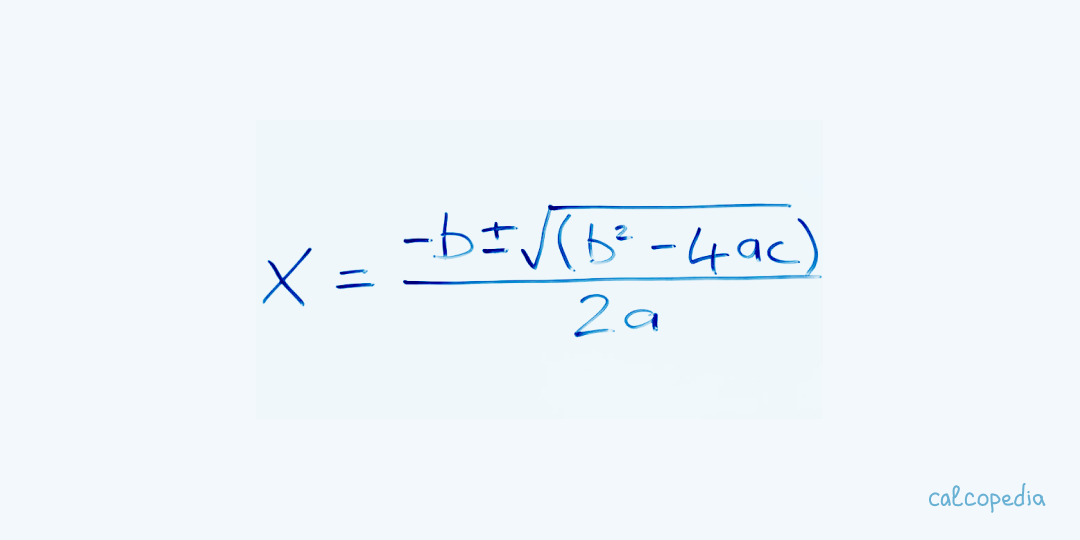
Квадратне рівняння — це рівняння вигляду ax² + bx + c = 0, де a, b та c — константи, а x представляє змінну. Такі рівняння називаються квадратними, оскільки невідомий x піднесено до квадрату, тобто до другої ступені.

Обчислення коренів квадратного рівняння — процес, що зазвичай включає в себе визначення значень змінної x, які задовольняють умови рівняння. Це означає, що підставляючи ці значення x назад у рівняння, ви отримаєте рівність.

Основний метод розв'язування квадратних рівнянь - це використання квадратного тричлену, відомого як формула квадратного кореня: x = (-b ± √(b²-4ac)) / (2a). Ця формула дає два можливі розв'язки, оскільки вона включає операцію "±", що вказує на наявність двох значень: одне з додаванням, а інше — з відніманням.

Інші методи розв’язування включають факторизацію та використання теореми Вієта, але ці методи можуть бути складнішими та не завжди застосовними.

Як користуватися калькулятором квадратних рівнянь?

Онлайн-калькулятор квадратних рівнянь — це потужний інструмент, який може значно спростити процес знаходження коренів квадратного рівняння. Ось кілька кроків, як правильно його використовувати:

1. Введення даних: Перш за все, вам потрібно ввести коефіцієнти a, b та c вашого квадратного рівняння у відповідні поля.

2. Перевірка даних: Переконайтеся, що введені вами дані є правильними та відповідають формату квадратного рівняння.

3. Розрахунок: Натисніть на кнопку для розрахунку, і калькулятор автоматично виконає всі необхідні обчислення, використовуючи відповідні формули.

4. Результати: Після обчислень ви одразу ж отримаєте корені рівняння, якщо такі існують, а також інформацію про дискримінант.

5. Аналіз результатів: Калькулятор також може надати інформацію про характер коренів (дійсні, уявні, однакові тощо) в залежності від значення дискримінанту.

6. Додаткові опції: Деякі калькулятори пропонують додаткові опції, такі як графічне представлення рівняння, що може допомогти в глибшому розумінні його структури та коренів.

Приклади обчислення квадратних рівнянь

Розглянемо декілька забавних та навчальних прикладів розв'язування квадратних рівнянь у реальному житті:

1. Кінематичне рівняння руху: Уявімо, що ви кидаєте м'яч угору, і вам потрібно дізнатися, на якій висоті м'яч буде через 2 секунди після кидка. За допомогою кінематичних рівнянь можна сформулювати квадратне рівняння, щоб знайти цю висоту, враховуючи прискорення вільного падіння.

2. Оптимізація ферми: Припустимо, ви маєте ферму і хочете встановити новий паркан таким чином, щоб максимізувати простір для ваших тварин, але при цьому використовувати мінімальну кількість матеріалів. Це може привести до квадратного рівняння, яке допоможе вам оптимізувати використання простору.

3. Кулінарні міркування: Нехай ви готуєте пиріг і хочете визначити, як радіус форми впливає на товщину пирога, знаючи, що об'єм залишається незмінним. Ви можете скласти квадратне рівняння для розрахунку цих розмірів, щоб ваш пиріг вийшов ідеальним!

Нюанси обчислення квадратних рівнянь

Хоча процес може здатися прямолінійним, існує кілька нюансів, на які варто звернути увагу під час розв'язування квадратних рівнянь:

1. Дискримінант може бути негативним, що вказує на відсутність дійсних коренів.
2. Якщо a = 0, рівняння не є квадратним, оскільки відсутній член з x².
3. Корені можуть бути комплексними, якщо дискримінант менший за нуль.
4. Подвійний корінь виникає, коли дискримінант дорівнює нулю.
5. Помилки округлення можуть вплинути на точність вашого розв'язку, особливо при роботі з дійсними числами.
6. Завжди перевіряйте свої розв'язки, підставивши їх назад у оригінальне рівняння.
7. Пам'ятайте про можливі обмеження в реальних ситуаціях, які можуть не враховуватися в чисто математичних обчисленнях.

Схожі калькулятори

Вам можуть бути корисними наступні калькулятори на цю ж тему:

• Калькулятор перетворення міліметрів в дюйми. Легко переводьте довжину з міліметрів в дюйми за допомогою цього простого онлайн-калькулятора.
• Калькулятор перетворення дюймів в міліметри. Швидко переводьте довжину з дюймів в міліметри з нашим зручним онлайн-калькулятором.
• Калькулятор перетворення сантиметрів в дюйми. Легко переводьте довжину з сантиметрів в дюйми з нашим онлайн-калькулятором.
• Калькулятор перетворення дюймів в сантиметри. 🔢 Переведіть дюйми в сантиметри за допомогою цього онлайн-калькулятора.
• Калькулятор тексту. З легкістю аналізуйте текст за допомогою цього онлайн-калькулятора, включаючи підрахунок символів та слів.
• Калькулятор абзаців у тексті. Швидко визначте кількість абзаців у вашому тексті з нашим онлайн-калькулятором.
• Калькулятор речень у тексті. Легко з'ясуйте кількість речень у вашому тексті з нашим простим онлайн-калькулятором.
• Калькулятор слів у тексті. Легко знайте кількість слів та унікальних слів у вашому тексті з цим простим онлайн-калькулятором.
• Тренажер ділення. Відточуйте свої навички ділення чисел з нашим зручним онлайн-тренажером.
• Тренажер з таблицями Шульте 7x7. Підвищуйте свою продуктивність і здібності скорочтення з таблицями Шульте 7x7.

Поділитися у соціальних мережах

Якщо вам сподобалося, поділіться калькулятором у своїх соціальних мережах. Це просто для вас і корисно для просування проекту. Дякуємо!