二次方程式とは何か、どのように計算するのか?
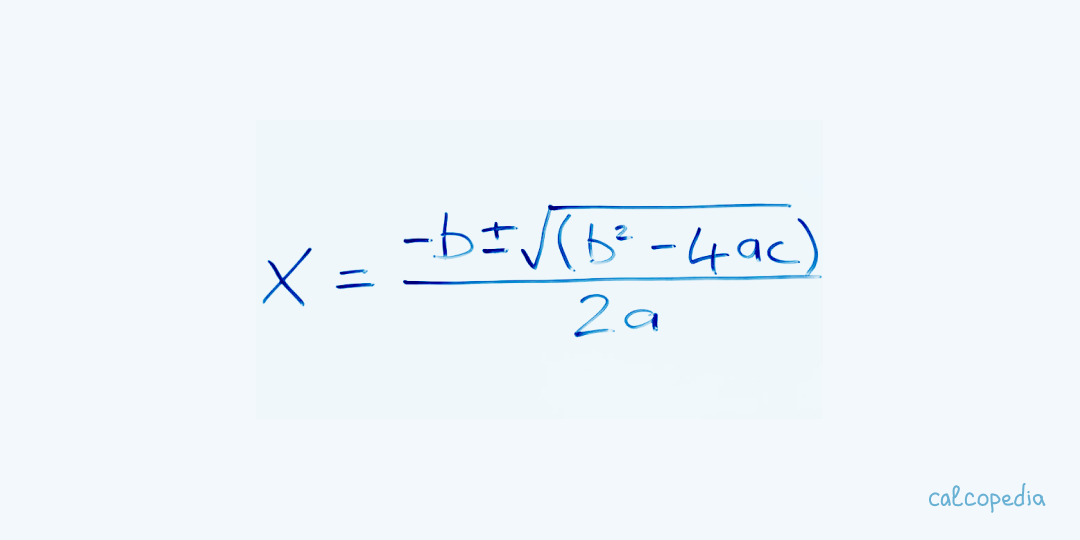
二次方程式とは、一般に ax² + bx + c = 0 の形式で表される方程式です。ここで、xは未知数を表し、a、b、cは実数で、aは0ではありません(a ≠ 0)。二次方程式は基本的に、方程式を解くことによって未知数の値を見つけ出す問題です。
二次方程式を解く方法はいくつかありますが、最も一般的なのは、係数a、b、cを使用して、判別式(またはディスクリミナント)を計算することです。判別式Dは b² - 4ac と計算され、この値によって方程式の解の数と性質が決まります。
具体的には、Dが0より大きい場合、方程式には2つの異なる実数解があります。Dが0の場合、方程式には重解(1つの解が2回現れる)があります。Dが0未満の場合、方程式には実数解がなく、2つの異なる複素数解があります。
また、二次方程式の解を見つける別の方法として、ベトの定理があります。この定理は、二次方程式の解の関係に関するもので、解の和と積を方程式の係数に関連付けます。
二次方程式計算機の使用方法
このオンライン二次方程式計算機は、誰でも簡単に二次方程式の解を見つけるのに役立ちます。以下は、このツールの基本的な使い方です。
1. まず、'a'、'b'、'c'のフィールドに、あなたの二次方程式の係数を入力します。
2. 次に、「計算」または同様のボタンをクリックします。
3. 計算機は自動的に判別式を計算し、可能な解の数とその値を提供します。
4. もし判別式が0以上の場合、計算機は2つの実数解を表示します。
5. もし判別式が0未満の場合、計算機は複素数解を提示します。
6. さらに、計算機はベトの定理を使用して、解の和と積の情報も提供することがあります。
7. 最後に、得られた解を確認し、必要に応じて新しい方程式の係数でプロセスを繰り返します。
二次方程式の計算例
ここでは、生活の中から抽出した二次方程式の具体的な例をいくつか紹介します。これらの例を通じて、二次方程式がどのように解かれるのかを理解できるでしょう。
1. 例:あなたの友人が誕生日パーティーのために花火を2つ上げます。花火は地上から高さ h(t) = -16t² + 64t + 9 (フィート)で上昇します。花火が最も高い位置に達する時間を求めます。
この場合、最大高度を求めるために、方程式を解く必要があります。これは、基本的に方程式の最大点を見つける問題です。計算機を使用すると、最大高度が得られ、その結果から最高点に達する正確な時間を計算できます。
2. 例:あなたはゲームのキャラクターとして、トレジャーハントに参加しています。宝物に到達するための道のりは、方程式 y = x² - 6x + 8 によって暗示されています。この問題を解決し、宝物を見つけるためのxの値を見つけます。
この興味深いシナリオでは、xの値を見つけるために方程式を解く必要があります。オンライン計算機は、あなたが宝物に到達するための正しい道のりを提供します。実際、これはゲームの中で最もエキサイティングな瞬間の一つかもしれません!
3. 例:ある日、あなたは月からの重力についてのジョークを思いつきました。地球上での重力方程式は g = 9.8 - 0.02h (hは高度)ですが、月ではどうでしょうか? 「それは簡単だ!」とあなたは言います。 「月の重力は、g = 1.6 - (あなたのお気に入りの数字)h のようなものだ!」
このユーモラスな状況では、あなたのお気に入りの数字を使って、実際に重力の減少を計算することができます。もちろん、これはジョークですが、二次方程式を解くことで、さまざまな物理的状況をモデル化することができることを示しています。
二次方程式を計算する際の注意点
二次方程式を解く際には、いくつかの重要な点を考慮する必要があります。これらの細かい点は、正しい解を得るために不可欠です。
1. 係数aは0ではないことを確認してください。aが0の場合、方程式は二次ではなく、一次になります。
2. 判別式が0未満の場合、方程式に実数解はありません。この時、解は複素数となります。
3. 方程式の係数が大きい場合、数値的な誤差に注意してください。計算機は理論上正確な値を提供しますが、実際の計算では誤差が発生する可能性があります。
4. 判別式が0の場合、方程式は重解を持ちます。これは、2つの解が同じであることを意味します。
5. 方程式を解く際に、すべての解が物理的な意味を持つとは限りません。解の実用性を常に考慮してください。
6. 二次方程式は、U字型のグラフ(放物線)を描きます。これは、最大値または最小値の問題を解決する際に役立ちます。
7. ベトの定理は、解の和と積を簡単に見つけるための強力なツールですが、方程式が特定の形式を持っている必要があります。
8. 方程式を解く際には、正しい単位を使用していることを確認してください。これは、物理問題や実世界のシナリオで特に重要です。
9. 常に解の検証を行ってください。計算機はツールですが、得られた解が問題の文脈に適合していることを確認するのはユーザーの責任です。
10. 異なる方法で方程式を解くことを試み、得られた解が一致するかどうかを確認してください。これにより、解の正確さが確保されます。
二次方程式の計算に関するよくある質問
二次方程式の判別式は何ですか?
判別式は、二次方程式の解の性質を決定するために使用される値です。具体的には、b² - 4ac という形式で計算され、この値によって解の数と種類(実数解または複素数解)が決まります。
複素数解とは何ですか?
複素数解とは、実数の範囲内で解くことができない方程式の解です。判別式が0未満の場合、二次方程式には実数解がなく、代わりに複素数解が得られます。
ベトの定理とは何ですか?
ベトの定理は、二次方程式の根(解)の和と積が、方程式の係数にどのように関連しているかを示す定理です。これは、方程式の解を素早く見つけるための便利な方法を提供します。
二次方程式計算機の精度はどの程度ですか?
二次方程式計算機は、理論的には非常に正確です。しかし、非常に大きなまたは小さな係数を持つ方程式を扱う場合、数値的な誤差が発生する可能性があります。
二次方程式の実用的な用途は何ですか?
二次方程式は、物理学(運動の法則など)、工学、経済学、天文学など、多くの科学的および実用的分野で広く使用されています。これらの方程式は、様々な現象をモデル化し、予測するのに役立ちます。
類似の計算機
同じトピックに関する次の計算機が役立つかもしれません:
- ミリメートルからインチへの長さ変換計算機. ミリメートルでの長さを入力し、インチに変換します。
- インチからミリメートルへの長さ変換計算機. インチでの長さを入力し、ミリメートルに変換します。
- センチメートルからインチへの長さ変換計算機. センチメートルでの長さを入力し、インチに変換します。
- インチからセンチメートルへの長さ変換計算機. インチでの長さを入力し、センチメートルに変換します。
- 数の進数変換計算機. 任意の数を入力し、選択した進数に変換します。
- 16進数から10進数への変換計算機. 16進数を入力し、10進数に変換します。
- 16進数から2進数への変換計算機. 16進数を入力し、2進数に変換します。
- 8進数から10進数への変換計算機. 8進数を入力し、10進数に変換します。
- 8進数から2進数への変換計算機. 8進数を入力し、2進数に変換します。
- 10進数から16進数への変換計算機. 10進数を入力し、16進数に変換します。
ソーシャルメディアで共有する
気に入ったら、計算機をソーシャルメディアプラットフォームで共有してください。あなたにとっては簡単で、プロジェクトのプロモーションにとっては有益です。ありがとうございます!