Zawartość
Czym jest długość okręgu i jak ją obliczyć?
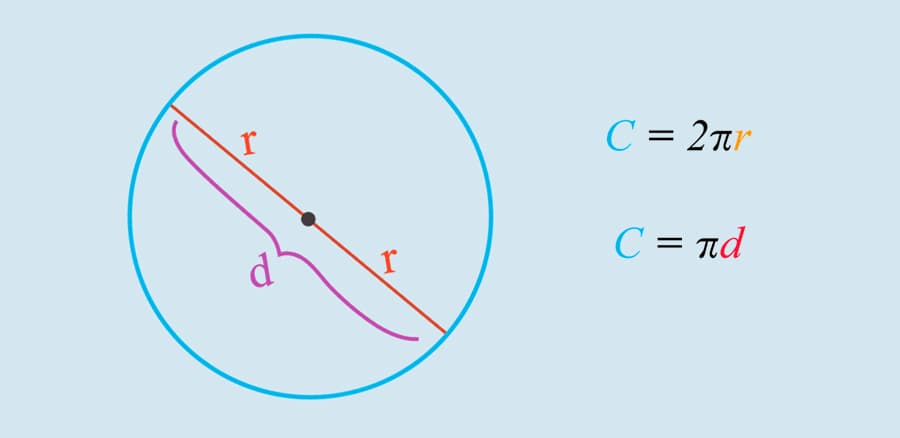
Długość okręgu to odległość wokół koła, którą można zmierzyć na jego obrzeżach. Jest to jedna z podstawowych miar w geometrii i matematyce.
Wyobraź sobie, że obchodzisz koło wokół jego brzegów; ścieżka, którą przejdziesz, to właśnie długość okręgu. Można ją obliczyć, znając pewne parametry koła, takie jak promień, średnica czy powierzchnia.
Najprostszą formułą na obliczenie długości okręgu (L) jest L = 2πr, gdzie r to promień koła. Alternatywnie, można użyć średnicy (d), gdzie L = πd.
Warto pamiętać, że π (pi) to stała matematyczna, która wynosi w przybliżeniu 3.14159, ale może być użyta z większą precyzją w zależności od potrzeb.
Jak korzystać z kalkulatora długości okręgu?
Nasz kalkulator jest prosty w użyciu i pozwala na szybkie obliczenia. Oto krok po kroku, jak go używać:
1. Wybierz, co znasz o kole: promień, średnicę czy powierzchnię.
2. Wpisz wartość wybranego parametru w odpowiednie pole.
3. Kliknij przycisk "Oblicz", aby uzyskać wynik.
4. Kalkulator wyświetli długość okręgu, a także inne interesujące informacje, jeśli będą dostępne.
5. Możesz eksperymentować, wprowadzając różne wartości, aby zobaczyć, jak zmienia się długość okręgu.
6. Pamiętaj, że wynik będzie tak precyzyjny, jak precyzyjne są dane wejściowe.
7. Możesz również skorzystać z dodatkowych funkcji kalkulatora, takich jak konwersja jednostek, jeśli jest dostępna.
Przykłady obliczania długości okręgu
Spójrzmy na kilka przykładów z życia wziętych:
1. Załóżmy, że masz koło o promieniu 5 cm. Używając formuły L = 2πr, obliczamy: L = 2 * 3.14 * 5 = 31.4 cm.
2. Teraz wyobraź sobie, że masz koło o średnicy 10 cm. W tym przypadku używamy formuły L = πd, co daje: L = 3.14 * 10 = 31.4 cm. Zbieg okoliczności? Nie sądzę!
3. A co, jeśli znasz powierzchnię koła? Załóżmy, że jest to 78.5 cm². Najpierw oblicz promień (r = √(A/π)), a następnie użyj go do obliczenia długości okręgu. Matematyka może być zabawna, prawda?
Nuanse obliczania długości okręgu
Istnieje kilka istotnych aspektów, które warto mieć na uwadze:
1. Upewnij się, że jednostki są spójne.
2. Pamiętaj, że wynik będzie tylko tak dobry, jak dane wejściowe.
3. Zaokrąglenia mogą wpłynąć na precyzję wyniku.
4. Wartość π użyta w obliczeniach ma kluczowe znaczenie.
5. W przypadku niestandardowych kół lub obręczy, obliczenia mogą być bardziej skomplikowane.
6. Różne kalkulatory mogą używać różnych metod zaokrąglania.
7. Pamiętaj o różnicy między średnicą a promieniem.
8. W przypadku dużych koł, błędy w pomiarach mogą być bardziej znaczące.
9. Obliczenia mogą być różne w zależności od tego, czy koło jest idealne, czy ma pewne nieregularności.
10. Warto czasem skorzystać z różnych metod obliczeń dla potwierdzenia wyniku.
Często zadawane pytania o obliczaniu długości okręgu
Czy mogę obliczyć długość okręgu, znając tylko powierzchnię koła?
Tak, ale najpierw musisz obliczyć promień koła z powierzchni, a następnie użyć go do obliczenia długości okręgu.
Czy wartość π jest zawsze taka sama?
Tak, π to stała matematyczna, która zawsze wynosi około 3.14159, ale można ją używać z różnym stopniem precyzji.
Co zrobić, jeśli mój wynik wydaje się być niepoprawny?
Sprawdź, czy poprawnie wprowadziłeś dane i czy użyłeś odpowiedniej formuły. Pamiętaj również o zaokrągleniach.
Czy ten kalkulator jest odpowiedni do obliczeń profesjonalnych?
Kalkulator jest świetnym narzędziem do szybkich obliczeń, ale dla precyzyjnych, profesjonalnych obliczeń warto skonsultować się z ekspertem.
Czy długość okręgu zawsze jest proporcjonalna do jego średnicy?
Tak, długość okręgu jest zawsze proporcjonalna do średnicy, co wynika z definicji liczby π.
Podobne kalkulatory
Następujące kalkulatory na ten sam temat mogą być przydatne:
- Kalkulator powierzchni sfery. Obliczaj powierzchnię sfery dla różnych zastosowań.
- Kalkulator powierzchni sześciokąta. Oblicz powierzchnię regularnych sześciokątów dla różnych zastosowań.
- Kalkulator powierzchni sześcianu. Oblicz powierzchnię sześcianu, korzystając z jego wymiarów.
- Kalkulator przeliczania skali. Łatwo przeliczaj skale na rysunkach technicznych na rzeczywiste wymiary.
- Kalkulator objętości prostopadłościanu. Obliczaj objętość prostopadłościanów dla różnych zastosowań.
- Kalkulator objętości sześcianu. Obliczaj objętość sześcianów dla różnych zastosowań, korzystając z naszego kalkulatora.
- Kalkulator objętości pomieszczenia. Obliczaj objętość pomieszczeń dla różnych potrzeb, korzystając z naszego kalkulatora.
- Kalkulator długości łuku. Oblicz długość łuku dla różnych potrzeb, korzystając z naszego kalkulatora.
- Kalkulator objętości rury. Oblicz objętość rur dla różnych zastosowań, korzystając z naszego kalkulatora.
- Kalkulator objętości piramidy. Oblicz objętość piramid dla różnych potrzeb, korzystając z naszego kalkulatora.
Udostępnij w mediach społecznościowych
Jeśli Ci się spodobało, udostępnij kalkulator w swoich mediach społecznościowych. To łatwe dla Ciebie i korzystne dla promocji projektu. Dziękuję!