Kuadratik Denklem Hesaplayıcı

Kare Denklemler Nedir ve Nasıl Hesaplanır?

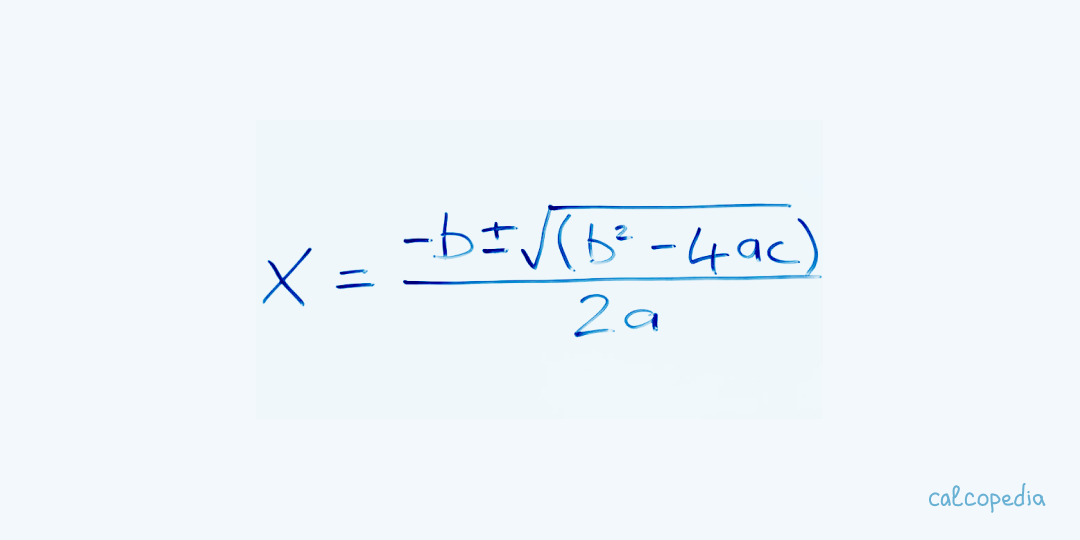
Kare denklemler, genel formülü ax² + bx + c = 0 şeklinde olan ikinci dereceden polinom denklemlerdir. Burada a, b ve c sabit sayılar olup a ≠ 0'dır. Bu tür denklemler, matematikte çok önemli bir yere sahiptir ve birçok farklı alanda kullanılırlar.

Kare denklemlerin çözümü için çeşitli yöntemler bulunmaktadır. Bunlar arasında en yaygın olanları; özel formüller kullanarak, diskriminant yoluyla ve Vieta teoremine dayalı çözümlerdir. Her yöntem, denklemin yapısına ve verilen koşullara göre avantajlar sunar.

Kare denklemlerin çözümünde diskriminant, Δ = b² - 4ac formülü ile hesaplanır. Diskriminantın değerine göre denklemin köklerinin durumu belirlenir. Örneğin, Δ > 0 ise iki farklı gerçek kök; Δ = 0 ise çakışık iki gerçek kök; Δ < 0 ise hiç gerçek kök yoktur.

Kare Denklem Hesaplama Aracı Nasıl Kullanılır?

Bu online araç, kare denklemleri hızlı ve kolay bir şekilde çözmenize yardımcı olur. Kullanımı basittir ve sadece birkaç adım gerektirir:

1. Öncelikle, denkleminizin katsayılarını (a, b, c) belirleyin.

2. Bu katsayıları ilgili alanlara girin.

3. 'Hesapla' butonuna basın.

4. Aracın, denkleminizin köklerini ve çözüm sürecini göstermesini bekleyin.

5. Eğer isterseniz, çözümü detaylarıyla inceleyebilir ve anlamaya çalışabilirsiniz.

6. Farklı denklemler için işlemi tekrarlayabilirsiniz.

Kare Denklemlerin Örnek Hesaplamaları

Gerçek hayattan alınmış kare denklem örneklerini ele alalım ve bunları nasıl çözeceğimizi inceleyelim:

Örnek 1: x² - 5x + 6 = 0 denklemini çözelim. Burada a=1, b=-5, c=6. Δ = (-5)² - 4*1*6 = 25 - 24 = 1. Δ > 0 olduğu için iki farklı gerçek kökümüz var. Kökler x1 = 3 ve x2 = 2.

Örnek 2: 2x² + 4x + 2 = 0 denklemini ele alalım. a=2, b=4, c=2. Δ = 4² - 4*2*2 = 0. Bu durumda, çakışık iki gerçek kökümüz var ve her ikisi de x = -1.

Örnek 3: x² + x + 1 = 0 denklemini inceleyelim. a=1, b=1, c=1. Δ = 1 - 4 = -3. Δ < 0 olduğundan, gerçek kök yoktur. Matematik bazen sürprizlerle doludur, değil mi?

Kare Denklemleri Hesaplarken Dikkat Edilmesi Gereken Nüanslar

Kare denklemleri hesaplarken dikkate alınması gereken bazı önemli noktalar vardır:

1. Katsayıların doğru girildiğinden emin olun.

2. Diskriminantı hesaplarken işaret hatalarına dikkat edin.

3. Köklerin gerçek, çakışık veya karmaşık olabileceğini unutmayın.

4. Denklemin derecesinin ikinci derece olduğundan emin olun.

5. Çözüm adımlarını adım adım takip edin.

6. Karmaşık sayılarla karşılaştığınızda paniğe kapılmayın.

7. Çözümü kontrol etmek için kökleri denkleme yerine koyun.

8. Eğer bir hata yaparsanız, adımları tekrar gözden geçirin.

9. Matematiksel düşünme ve problem çözme becerilerinizi geliştirmeyi unutmayın.

Kare Denklemler Hakkında Sıkça Sorulan Sorular

Benzer hesap makineleri

Aynı konuda aşağıdaki hesap makineleri faydalı olabilir:

• Sayı Sistemleri Dönüşümü. Bir sayı girin, seçtiğiniz sayı sistemleri arasında çevrimiçi dönüşüm yapın.
• Onaltılı-Ondalık Dönüşüm. Onaltılı sayı girin, ondalık karşılığını çevrimiçi hesaplayın.
• Onaltılı-İkili Dönüşüm. Onaltılı sayı girin, ikili karşılığını çevrimiçi hesaplayın.
• Sekizli-Ondalık Dönüşüm. Sekizli sayı girin, ondalık karşılığını çevrimiçi hesaplayın.
• Sekizli-İkili Dönüşüm. Sekizli sayı girin, ikili karşılığını çevrimiçi hesaplayın.
• Ondalık-Onaltılı Dönüşüm. Ondalık sayı girin, onaltılı karşılığını çevrimiçi hesaplayın.
• Ondalık-Sekizli Dönüşüm. Ondalık sayı girin, sekizli karşılığını çevrimiçi hesaplayın.
• Ondalık-İkili Dönüşüm. Ondalık sayı girin, ikili karşılığını çevrimiçi hesaplayın.
• İkili-Onaltılı Dönüşüm. İkili sayı girin, onaltılı karşılığını çevrimiçi hesaplayın.
• İkili-Sekizli Dönüşüm. İkili sayı girin, sekizli karşılığını çevrimiçi hesaplayın.

Sosyal medyada paylaş

Beğendiyseniz, lütfen hesap makinesini sosyal medya platformlarınızda paylaşın. Siz için kolay ve projenin tanıtımı için faydalıdır. Teşekkürler!